こんにちは、ヤツPです!
突然ですが、「日本に電柱は何本あるでしょう?」こんな突拍子もない質問にどう立ち向かいますか? 実はこれ、コンサルティングファームの採用面接でもおなじみの問い。それが「フェルミ推定」です。
フェルミ推定とは、あらかじめ知識として持っていない数値に対して、自らの知識と論理を組み合わせて概算を導き出す思考法。つまり、ただの計算問題ではなく、「思考の筋力」をチェックするシミュレーションであり、コンサルタントにとって必須の基礎技術でもあります。
特にケース面接の冒頭で出されるフェルミ推定は、その後の戦略議論につながる「構造化された思考」の出発点として重視されています。いわば、フェルミ推定はコンサル的思考法の“足腰”なのです。
ここでは、特に薬剤師にとっては馴染みがないフェルミ推定について、フェルミ推定の定義と背景、コンサルがなぜ重要視するのか、典型的な問題例、思考の定石、さらには解法プロセスに至るまで丁寧に解説していきます。これからコンサルを目指す薬学生の皆さんにとって、必携の“思考道具”となるはずです。
フェルミ推定とは
フェルミ推定とは、「知識として持っていない数値に対して、論理的思考を駆使して妥当な概算値を導き出す技術」です。
ここで重要なのは、「知識として持っていない」という点。つまり、インターネット検索や専門知識が使えない状況で、ゼロからどこまで推論で近づけるかが問われます。
この推定法の名前は、20世紀を代表する物理学者エンリコ・フェルミに由来しています。彼は第二次世界大戦中、実験の最中に放出された中性子の数を、目に見える証拠と簡単な数学で概算したことで有名です。

写真は、イタリアの物理学者エンリコ・フェルミ
 灰原 哀
灰原 哀つまり、“知っているふり”をするんじゃなくて、“知らなくても考えられる”が重要ってこと。中途半端な知識より、筋の通った推論のほうがよほど価値があるわ。
フェルミ推定は、計算よりも構造化された思考や仮説構築、情報の整理力を問うもので、コンサル的思考トレーニングには最適です。
なぜフェルミ推定がケース面接の登竜門なのか
コンサルティングファームでは、フェルミ推定を通して候補者の「思考の骨格」が備わっているかを見極めています。具体的には、次の4つのコアコンピテンシーを観察しているのです。
- 仮説思考力
不確実な状況下で、「おそらくこうではないか」という仮の結論(仮説)を立て、それをもとに逆算的に検証していく力です。 - フレームワーク思考力
問題をMECE(漏れなく・ダブりなく)に構造化し、全体像を捉えながら要素ごとに分解して考える力です。これは後の戦略検討にも直結します。 - 論理的思考力と説明力
設定した仮定や分解に基づき、「なぜそう考えたのか」を明確かつ説得力ある言葉で説明する力。答えだけでなく、プロセスが評価対象です。 - 修正力
面接官からのフィードバックや新たな情報に応じて、自分の思考を柔軟に修正し、構造をアップデートできるか。これは現場のコンサルワークでも極めて重要です。
フェルミ推定は、これら4つすべての能力が露わになる設問です。たとえば、「この市場の売上を3年で1.5倍にするには?」といった設問に続くケース面接では、フェルミ推定で構築した市場モデルがそのまま議論の土台になります。
「顧客数 × 購入頻度 × 平均単価」という構造を自分で組み立てたうえで、どのレバーをどう動かすかを戦略的に語る。ここで“的外れな推定”をしていたら、その後の展開も破綻してしまうわけです。
このように、フェルミ推定は「論理構造の基盤」を築くプロセスであり、ケース面接全体のクオリティを左右する決定的なステップなのです。



仮説があることで、情報収集や議論が“狙い撃ち”になる。全方位に広げるのは非効率ですからね。
例題で学ぶフェルミ推定
ここからは実際に、フェルミ推定がどのように使われるのか、具体的な例題を使って考えてみましょう。なお、解法の中で「構造化」や「仮説の立て方」などにも注目してみてください。
なお大前庭として、フェルミ推定の回答は1つとは限りません。ロジックに筋が通っていてある程度の精度で推定できれば良いということを認識してください。
なお、コンサルの選考を一つの場面として考えると「短時間で解く」ということも非常に重要になってきます。
例題1:日本に電柱は何本あるか?(回答目安:5分間)



ワシの家の前にも電柱が2本あるんじゃが、あれを基準にしてもよいのかのう?
まず、日本の電柱の総数を推定するには、電柱の“密度”と日本の“面積”を掛け算するアプローチが多いですね。ここでは、次のような思考プロセスを選択します。
- 日本の国土面積は約38万平方キロメートル。
- 山間部:都市部の比率は、森林面積に基づいておよそ7:3と仮定。
- 都市部では、50メートル四方ごとに電柱が1本あるとすると、1平方キロメートルあたり400本。
- 山間部は200メートル四方ごとに1本、すなわち1平方キロメートルあたり25本。
これを式に落とし込むと:
電柱の本数 =400本 × 38万平方キロ × 0.3(都市部)+25本 × 38万平方キロ × 0.7(山間部) = 約5,225万本



実際の本数は約3,500万本らしいけど、これでも“桁”が合っていれば十分とされるのがフェルミ推定よ。目的は“精度”より“構造”だから。
このように、仮定を置きながら構造的に解を導くプロセスがフェルミ推定の本質なのです。
例題2:東京都のマンホールはいくつあるか?(回答目安:5分間)
こちらも良く出てくる例題ですね。今度は人口ベースの推定してみます。
- 東京都の人口:1,400万人
- 1世帯あたり2人 → 世帯数:700万世帯
- 10世帯に1つマンホールがあると仮定
これらから、
東京都のマンホール数 = 700万世帯 ÷ 10世帯/個 = 70万個
実際の都内マンホール数は約48.5万個(2015年時点)となっております。
例えば、15世帯に1つのマンホールと設定すれば近似値にはなるものの、ここでは思考のプロセスが重要となりますので、結果としては許容範囲となります。
例題3:日本にあるコンビニの数は?(回答目安:5分間)
ここでは面積と密度に着目して推定してみます。
- 日本の国土:380,000 km²
- 都会(1割)→ 0.25km²に1軒(4軒/km²)
- 田舎(9割)→ 2.5km²に1軒(0.4軒/km²)
- 森林など住居不可エリア(20/30)→ほぼゼロ
計算式:
都市部:38万 × (1/30) ÷ 0.25 = 約5,067軒
田舎 :38万 × (9/30) ÷ 2.5 = 約45,600軒
となり、合計では50,667軒と計算されます。
実際のデータ:全国で約57,000軒。こちらも推定にしては健闘している数字です。



大事なのは“どこから着眼するか”と“どの精度で分けるか”。一見ランダムな問いも、筋道立てればここまで近づけるんだ。
例題4:東京のラーメン店の一日の売上は?(回答目安:5分間)
こちらは、売上 = 【席数】×【稼働率】×【回転率】×【営業時間】×【客単価】
として考えてみます。
さらに仮定として下記とします:
- 席数:10席
- 稼働率:1(常に満席)
- 回転率:2回転/時間
- 営業時間:12時間(11:00〜23:00)
- 客単価:1,000円
売上 = 10席 × 1回転 × 2回転/時間 × 12時間 × 1,000円 = 240,000円/日
と考えられます。稼働率が1の人気店としていますが、例えば稼働率が半分の店なら売上も5割下がる推定となります。



この分解式がポイントですね。売上の“レバー”を分けて考えると、感覚ではなく根拠で話せるようになります。
例題5:日本の缶コーヒーの市場規模は?(回答目安:5分間)
次は少し試算する市場規模が大きくなります。
仮定:
- 日本人口:1.2億人
- 就業層をターゲットとする
- 男性就業者(18~65歳):150万人×48年÷2≒3,600万人
- 女性就業者(18~65歳):150万人×48年÷2×0.7≒2,520万人
※専業主婦などを考慮して70%割合 - 男性シニア層(66~80歳):150万人×15年÷2=1,125万人
※女性就業者については専業主婦などを考慮して70%とする
※平均寿命は約80歳として各年齢層は一律に分布していると仮定(※簡略化のため)し、150万人/歳で試算
※シニア層は男性のみを想定
- 購入頻度と単価:
- 男性(週2回/年104回 × 140円)
- 女性(週1回/年52回 × 140円)
- シニア(年26回 × 140円)
計算:
3600万人 × 104 × 140円 = 約5,200億円
2520万人 × 52 × 140円 = 約1,800億円
1125万人 × 26 × 140円 = 約410億円
合計 ≒ 7,410億円
実際の市場規模もおおよそ7,000〜8,000億円規模であり、結果としては近い数字になりました。スタバやコンビニの影響をする人もいれば、レバーとして自販機やコンビニ、スーパーなどの販売量から推定する人もいるかと思いますが、あくまで思考プロセスが重要となります。
フェルミ推定には定石がある
ストック型 vs フロー型
フェルミ推定には、問題のタイプによって「分類の定石」が存在します。特に有名なものが「ストック型」と「フロー型」の分類です。
❶ストック型:ある時点で「存在している数」を問う問題
例:日本にある電柱の本数、コンビニの数、スマホの保有台数
❷フロー型:ある期間内に「流れる量」を問う問題
例:1日あたりのラーメン店の売上、1年間の缶コーヒー市場規模



ワシのエアコンも“ストック型”ってやつかのう? まだ現役じゃよ!
ストック型は所持型と非所持型にさらに分けられる
さらに、ストック型はより細かく次の2つに分けると、アプローチが立てやすくなります:
❶‐2:「所有数を問うタイプ」:人口・世帯ベースでアプローチするのが有効
例:スマートフォン、冷蔵庫、エアコン、ゲーム機
❶‐2:「設置数・存在数を問うタイプ」:面積ベースでアプローチするのが有効
例:マンホール、信号機、自販機、電柱
なぜこのように分けるのかというと、計算の入口(レバー)が異なるためです。
- 所有に基づくもの → 人口、世帯、年齢層、普及率など
- 存在に基づくもの → 国土面積、都市部密度、地理的比率など
この「切り口の分類」が早期にできるようになると、問題の構造化にかかる時間が大幅に短縮され、より深い洞察へとつなげることが可能になります。
フロー型はミクロ視点とマクロ視点に分けられる
フェルミ推定において「フロー型」の問い――つまり、ある一定期間における売上や流通量、消費量を問う問題――では、さらに ミクロ視点 と マクロ視点 の二つのアプローチに分けて考えると、精度がぐっと高まります。
ミクロ視点 × 供給側(売り手視点)
たとえば、「東京のラーメン店1店舗の1日の売上はいくらか?」という問いに取り組む場合は、供給側(売り手)の視点から考えるのが効果的です。
対象とする店舗の客層を細かく定義するのは難しく、一方で「現場単位の収益構造」は、実際に提供されるサービスのキャパシティ――座席数、回転率、営業時間、客単価といった供給能力に強く依存することもあり供給側視点で考えていくのが定石となります。
マクロ視点 × 需要側(買い手視点)
一方で、「日本の缶コーヒーの市場規模は?」のように、社会全体にわたるボリュームを問うようなマクロ視点の問いにおいては、需要側(買い手の視点)からのアプローチが有効です。
なぜなら、缶コーヒーのような大量消費される嗜好品は、チャネル(自販機・コンビニなど)や地域を限定せず、広範な人口セグメントに分散して消費されるからです。
このようなケースでは、
市場規模 = 消費者数 × 購入頻度 × 単価
また、年齢・性別・職業などの属性ごとにセグメントを切ることで、仮定を細かく設定することができ、精度の高い推定が可能になります。
ストック型 vs フロー型
まとめると、下記の通りになります。
あくまでアプローチの入口の一つではありますが、面接などでは限られた時間で回答を導く必要があるため、多くの方が定石として認識しております。
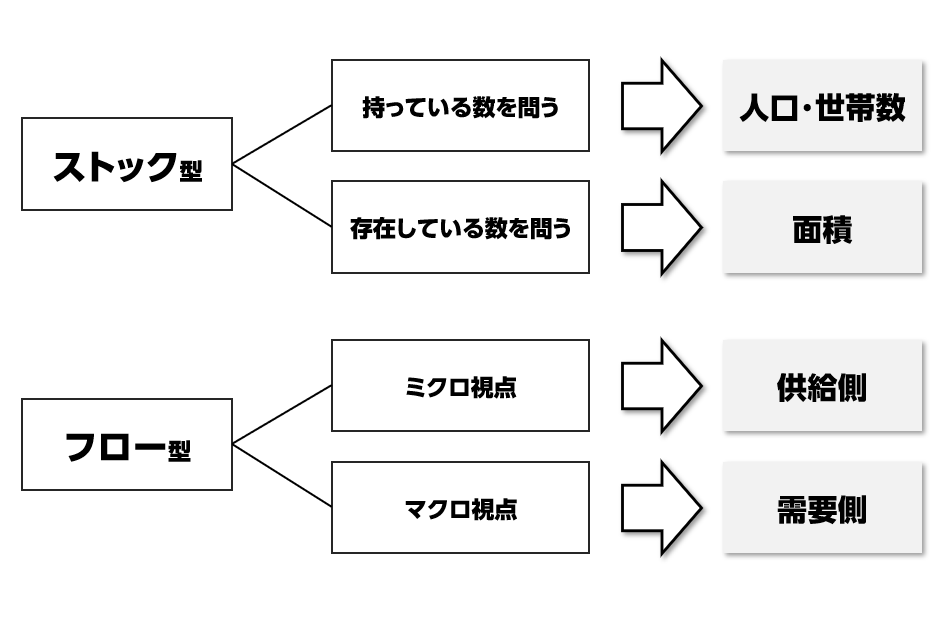

図:フェルミ推定の定石
フェルミ推定の4ステップ(考えるステップ)
フェルミ推定は、闇雲に数字を当てはめていくような作業ではなく、明確な「思考プロセス」を通じて仮説を構築していくものです。基本ステップは4つとなります。
1. 前提確認
問題の定義や範囲(スコープ)を明確にする。
これは最初のステップですが、軽視されがちです。問題設定の段階であいまいな部分をそのままにしてしまうと、以降の推定がブレてしまいます。



えっ、水って“水道水”のこと?それとも“ペットボトルの水”のこと…?
たとえば、「コンビニ1店舗の1日の飲料水の売上本数を推定せよ」と言われた場合を考えてみましょう。
この「飲料水」が、
- お茶や炭酸飲料を含むすべてのドリンクを指すのか?
- それとも“ミネラルウォーター”のような、狭義の「水」を指すのか?
によって、想定すべき客層・販売本数が大きく変わります。さらに、
- 対象の店舗が住宅地にあるのか?
- それとも地方の幹線道路沿いにあるのか?
でも来店数は変化するでしょう。このように、スコープを明確にすることは論理のブレを防ぎ、推定の質を高める土台となります。
前提が不明瞭な場合、自らの意思で「仮定を置く」姿勢が問われます。
例:「この問題では“ミネラルウォーター”のみを対象とし、店舗は都市部の住宅地に立地していると仮定します」
2. 構造化
問題を構成する要素に分解し、計算可能な数式モデルを組み立てる。
構造化とは、問題を「数式」に落とし込める状態にまで分解する作業です。ここで重要なのは、
- 何が売上や個数に影響しているか(レバー)を明確にする
- それらが掛け算 or 足し算のどちらで結びついているかを明示する ことです。
上記の例題を用いて考えると、
1日の飲料水売上本数 = 来店客数 × 飲料購入率 × 1会計あたり購入本数 × 水のカテゴリ比率
このように因数分解していくと、それぞれの変数に対して具体的な数値の仮定を置く準備が整います。
3. 数値設定
分解した各要素に、論理的根拠のある仮定数値を設定する。
このフェーズでは「その数字をどうしてそう仮定したのか?」の理由づけが大切です。自分の感覚や普段の観察から引用するケースも少なくありませんが、いずれにしても何かしらの根拠を持つことが大切になります。
例:
- 都市部コンビニ → 来店数:700人/日
- 飲料購入率:32%(感覚的に3人に1人程度)
- 1会計あたり:1.05本(まとめ買いも少しあり)
- 水カテゴリ比率:20%(コーヒーやジュースの方が多いため)



妥当性のない数字に意味はないわ。“なんとなく”は推定じゃなくて妄想よ
4. 計算実行
設定した数値を掛け合わせて、最終的な数値を算出。
ここでは、各変数の整合性を保ちながら丁寧に計算していくことが求められます。
例:700人 × 32% × 1.05本 × 20% ≒ 47本/日(1店舗のミネラルウォーター売上)
また、算出後には結果の“桁”や“オーダー感”が現実的かどうかを再検証するのが重要です。現実のデータと比較して、「このズレは仮定のどこに起因するか?」を自己レビューする習慣を持ちましょう。
この4ステップは、フェルミ推定をただの“あてもの”ではなく、論理的な思考演習へと引き上げてくれます。
フェルミ推定を学ぶならコレ!
フェルミ推定を学ぶド定番!複雑な問題を分解し、仮説を立てて答えを導く思考法を学べる一冊。電柱の数やピザ消費量など実践的な問題を通じて、論理的思考力と地頭力を鍛えます。就活やコンサル面接対策には必須です。
こちらもド定番です。単なる論理の積み上げではなく、不確実性の中で未来を描くための発想法を解説する一冊として、ロジックに加え直観・仮説・全体観を統合しビジネスにおける本質的な意思決定力を養うサポートになります。
思考の瞬発力・仮説構築力・抽象化力といった「地頭力」の基本を体系的に解説したベストセラーです。日常の課題をシンプルに捉え、答えの出ない問いに挑む力を磨け、フェルミ推定ノートが実践演習型、戦略思考が未来志向型であるのに対し、こちらは基礎編としての入門書的な位置づけです。
フェルミ推定は「思考の武器」になる
フェルミ推定は、「答えを知っているかどうか」ではなく、「答えにどこまで近づけるか」を試す思考訓練です。コンサルタントとして必要な“考える筋肉”を鍛えるには、この推定を繰り返すことが何よりも効果的です。



結論にたどり着く速さよりも、“どうやってそこに至ったか”のプロセスを語れることが、真に信頼される思考力を意味する。



フェルミ推定は、問いに対する“物語”を構築する練習でもあるんだ。論理をつないで、世界を描ける力を磨こう。
次回は、実際にファームで出題されたフェルミ問題を使いながら、実践形式で解いていきましょう。お楽しみに!





コメント